
DiffusionModel扩散模型
Diffusion Model 扩散模型
参考视频:强推!不愧是公认的讲的最好的【Diffusion模型全套教程】同济大佬3小时带你从入门到进阶(深度学习/神经网络/GAN/Diffusion模型)_哔哩哔哩_bilibili
markdown中公式书写:如何在简书Markdown中输入数学公式 - 简书 (jianshu.com)、Markdown常用数学公式_nanyidev的博客-CSDN博客_markdown 数学公式
¶❤️🔥 前置:正态分布
¶1、基本概念
服从正态分布可表示为:
$$
Z\sim N(0,1)
$$
其中,μ=0,σ=1
具体参数及含义如下表:
| 参数 | 含义 |
|---|---|
| μ | 均值;期望 |
| σ | 标准差 |
| $σ^2$ | 方差 |
方差公式:
- 标准差^2
- 其含义为与均值的距离的均值。由于减去(距离的均值)结果有正有负,所以添上平方
- 式子🍒可以翻译成式子🍏,即对(数字xi减去均值x拔的平方)求均值
$$
🍒σ^2=E[(X-E(x))^2]🍒
$$
方差公式也可写为:
$$
🍏σ^2=\frac{\sum_{i=1}^{n}(x_i-\overline{x})^2}{n}🍏
$$
从该式子中可以进行的解读是:方差=(数据与均值之间)平均距离
¶2、图像表示
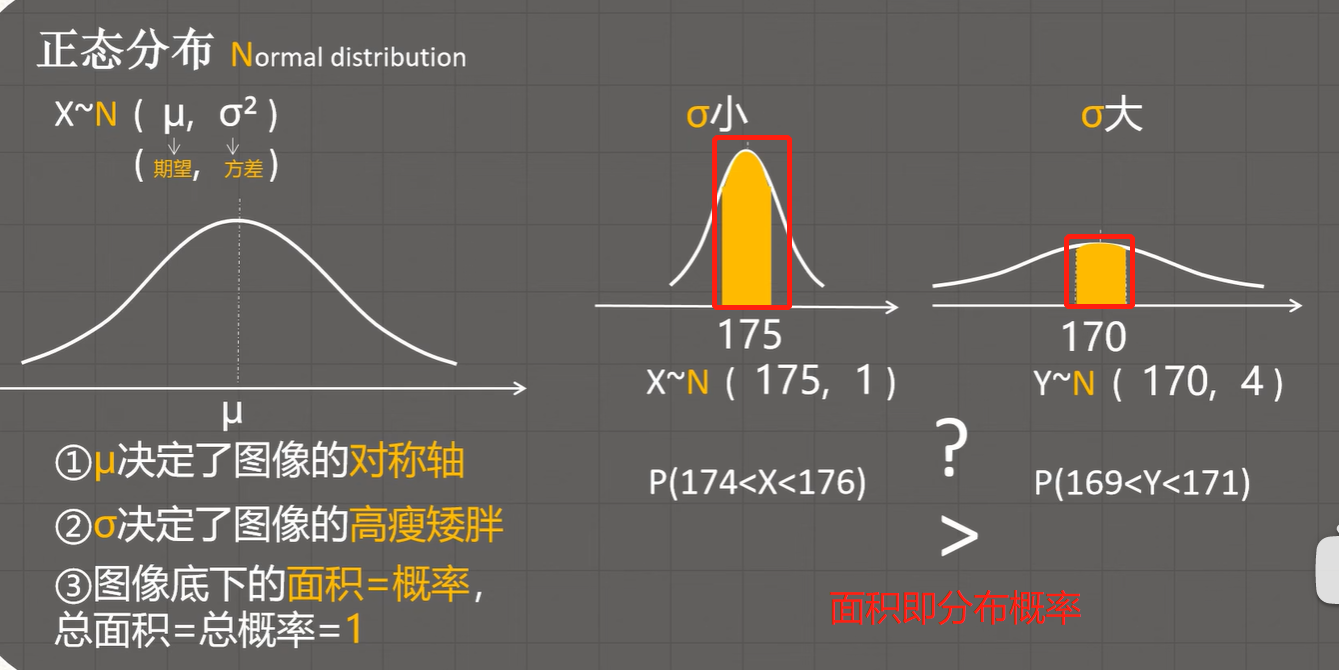
正态分布图像:方差越小,数据越集中;方差越大,数据越分散
¶3、运算法则
➕加法➕:①如果两个相互独立的正态分布X~N(u1,m),Y~N(u2,n),那么Z=X±Y仍然服从正态分布:
$$
Z\sim N(u1±u2,m+n)
$$
➕加法➕:②正态分布加一个常数,还是符合正态分布,只是期望值加上了这个常数:
$$
N(0,σ²)+C \sim N(C,σ²)
$$
❌乘法❌:在标准正态分布前乘以一个常数后,服从如下分布:
$$
aX\sim N(0,a^2)
$$
¶🎣 流程概述
扩散模型建模整体分为两个步骤:
- 前向加噪。一共n个时刻,每个时刻都向图像中添加噪声,噪声满足标准的正态分布。噪声本质上就是标签。
- 后向去噪。知道了怎么加噪声就知道怎么还原图像。
¶🪀 前向加噪
从X0时刻开始,依次向图像中添加噪声。而每个时刻加的噪声量是不一样的,因为我们希望每个时刻加了噪声之后,图像的扩散幅度是一样。前面时刻的图像加一点点肉眼就能看出扩散幅度,后面时刻的图像中噪声分布得已经极没有规律了,如果还加一点点噪声,那就完全没有效果,看不出扩散幅度了。所以往后,加的噪声是越来越多的。即,越往后噪声的影响越大,上一时刻的状态影响越小。

假设β是每幅图像噪声加成的权重项,β值在0.0001-0.002范围内自己调,我们令:
$$
α_t=1-β_t
$$
某一时刻的分布Xt计算公式如下所示:
$$
🍓X_t=\sqrt{α_t}x_{t-1}+\sqrt{1-α_t}z_1 🍓
$$
某一时刻的分布=权重1*上一时刻的分布+权重2*新输入的噪声。越往后噪声的权重越大,上一时刻的分布的权重越小。已知X0,要想求出Xt时刻的分布,得通过递归的方式,先求Xt-1再求Xt-2以此类推,很像RNN,只能串行,效率低 (这也是RNN后来被Transformer取代的原因之一)。所以我们期望,通过X0,不考虑中间其他时刻噪声的分布,而直接求出Xt。
🦖推导过程:
先求出Xt-1的分布瞅瞅:
$$
X_{t-1}=\sqrt{α_{t-1}}x_{t-2}+\sqrt{1-α_{t-1}}z_2
$$
Xt-1代入🍓式中得🎃:(其中z1z2都满足标准的正态分布)
$$
🎃X_t=\sqrt{α_tα_{t-1}}x_{t-2}+\sqrt{α_t(1-α_{t-1})}z_2+\sqrt{1-α_t}z_1🎃
$$
由于z1、z2均为服从(0,1)的正态分布,两者前面乘上一个常数后服从的分布为:
$$
\sqrt{1-α_t}z_1\sim N(0,1-α_t)
$$
$$
\sqrt{α_t(1-α_{t-1})}z_2\sim N(0,α_t(1-α_{t-1}))
$$
两者相加后服从的正态分布为:
$$
\sqrt{1-α_t}z_1+\sqrt{α_t(1-α_{t-1})}\sim N(0,1-α_tα_{t-1})
$$
还原到式子🎃中得(其中z2拔表示为一个标准正态分布,所以等同于z1):
$$
X_t=\sqrt{α_tα_{t-1}}x_{t-2}+\sqrt{1-α_tα_{t-1}}\overline{z}_2
$$
观察该式与🍓式子:
$$
🍓X_t=\sqrt{α_t}x_{t-1}+\sqrt{1-α_t}z_1 🍓
$$
发现想求xt-2时,仅在根号下跟着αt后面跟着乘一个αt-1即可。由此推出:
$$
🐨X_t=\sqrt{\overline{α}_t}x_0+\sqrt{1-{\overline{α}_t}}{z_{t}}🐨
$$
其中α拔为α的累乘,zt为标准正态分布,x0为原始图像分布,任意时刻的XT可以由此式求出
¶🎐 反向去噪
目标:希望通过知道Xt的分布反向推导出X0,但直接推出来是不现实的。所以我们慢慢通过推导Xt-1、Xt-2如此迭代下来到X0
首先努力通过已知Xt的分布(后一时刻)反向推导出Xt-1的分布(前一时刻)。我们使用到贝叶斯公式进行转换。
贝叶斯公式:已知由A分布求出的B分布,可以逆转,由Xt-1分布倒推出Xt分布
$$
P(A|B)=P(B|A)\frac{P(A)}{P(B)}
$$
运用到这里来就是:已知由Xt分布求出的Xt-1分布,可以逆转,由Xt-1分布倒推出Xt分布
$$
q(X_{t-1}|X_t,X_0)=q(X_t|X_{t-1},X_0)\frac{q(X_{t-1}|X_0)}{q(X_t|X_0)}
$$
式中添加上X0是因为后面的Xt-1和Xt的分布都需要根据X0求出
对每一项分布进行拆解:
$$
q(X_t|X_{t-1},X_0):🍓X_t=\sqrt{α_t}x_{t-1}+\sqrt{1-α_t}z 🍓\sim N(\sqrt{α_t}x_{t-1},1-α_t)
$$
$$
{q(X_{t-1}|X_0)}:🐨X_{t-1}=\sqrt{\overline{α}_{t-1}}x_0+\sqrt{1-{\overline{α}_{t-1}}}{z}🐨\sim N(\sqrt{\overline{α}_{t-1}}x_0,1-{\overline{α}_{t-1}})
$$
$$
{q(X_t|X_0)}:🐨X_t=\sqrt{\overline{α}_t}x_0+\sqrt{1-{\overline{α}_t}}{z}🐨\sim N(\sqrt{\overline{α}_t}x_0,1-{\overline{α}_t})
$$
正态分布N(μ,σ2)的公式如下所示:
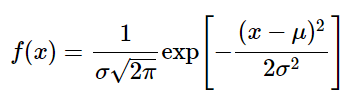
将以上正态分布代入到公式后化简,整理成以下形式再一一对应,就可以得到σ2(是个常数)

已知σ2的值后,按照下面蓝框的形式,给上面蓝框乘上σ2再除以2,就可以得到期望μ的值,解出μ如下:
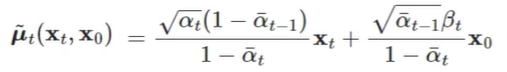
X0可以通过🐨式子推导出来:
$$
🐨X_t=\sqrt{\overline{α}_t}x_0+\sqrt{1-{\overline{α}_t}}{z_{t}}🐨
$$
$$
X_0=\frac{1}{\sqrt{\overline{a}_t}}(X_t-\sqrt{1-{\overline{a}_t}}z_t)
$$
带入式中得μ:
$$
\tilde{μ}_t=\frac{1}{\sqrt{a_t}}(x_t-\frac{β_t}{\sqrt{1-\overline{a}_t}})z_t
$$
但此时,我们唯一不知道的量就是zt,即每个时刻加入的噪声
¶🦔 噪声建模
科学家们无法通过数学公式去推导出噪声,只能让机器利用深度学习去猜,利用模型去预测$z_t$,我们的前向过程中,向图像中加入的每一步噪声,都是我们自己通过采样得到的已知值,通过该已知值去拟合我们未知的$z_t$
原始论文中是使用Unet这样的模型进行预测。每一时刻都需要Unet去推测前一时刻的$z_t$,由于输入不同,每个Unet也是不同的
¶🍧算法流程图

¶训练
$X_0\sim q(X_0) \quad$ 对数据集进行采样,即取数据
$t\sim Uniform({1,…,T}) \quad$ 构建一个t属于的序列,我们需要给每个batch扩散随机的次数,以防机器学到规律
$\varepsilon\sim N(0,I) \quad$ 噪声严格符合标准正态分布
$\nabla_{\theta} \lvert\lvert\varepsilon-\varepsilon_\theta(\sqrt{\overline{α}_t}x_0+\sqrt{1-{\overline{α}_t}}{\varepsilon})\lvert\lvert^2 \quad$ 整个式子表示梯度下降更新$\theta$权重参数。其中,$\varepsilon_\theta$为训练噪声的模型,模型中第一个参数是$X_t$时刻的图像,模型中第二个参数是告诉模型处于哪到哪第几幅图噪声的传播
¶采样
$X_t\sim N(0,I) \quad$$X_t$为在标准正态分布中随机采样的一个数值
$t=T,…,1 \quad$for循环
最后一步不加噪音点
$X_{t-1}$后面的公式就是利用之前求出的均值和方差进行计算的。我们通过此公式持续训练$X_{t-1}$、$X_{t-2}$,结果不断往前传,直到训练出$X_0$
